球体の体積の求め方を覚える 球体の体積の求め方は「4/3πr 3 」です。 「π」は円周率あるいはパイ、「r」は半径を指します。 例えば「3分の4かけるパイアール3乗」と覚えてしまいましょう。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4 π r 2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac{4}{3}\pi r^3 3 4 π r 3 →「身の上に心配アール三乗」 表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。 優雅 球体 表面積 求め 方 球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説し 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学び 球の表面積と体積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法

球の表面積と体積の公式 数学fun
球体の体積の求め方 公式
球体の体積の求め方 公式-円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事球の体積を求める公式は、V = 4/3 πr^3 で表されます。 このページでは、例題と共に、この公式の使い方を説明しています。 お使いのブラウザでは JavaScript が無効になっています。




球の表面積 なぜ
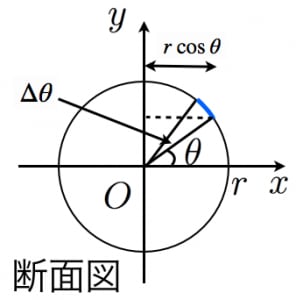
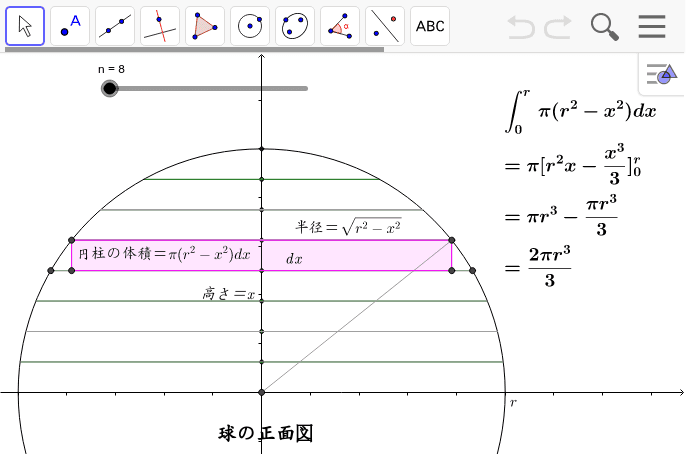
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして球体の体積の求め方を覚える 球体の体積の求め方は「4/3πr 3 」です。「π」は円周率あるいはパイ、「r」は半径を指します。 「π」は円周率あるいはパイ、「r」は半径を指します。 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, 中学数学 なぜ4pr 2で 表面積が求められるのか Youtube 球体表面積公式
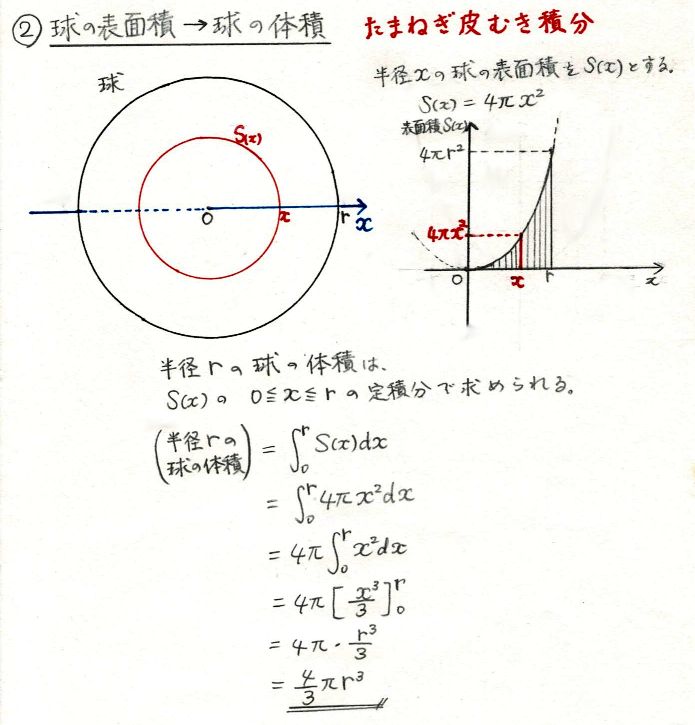
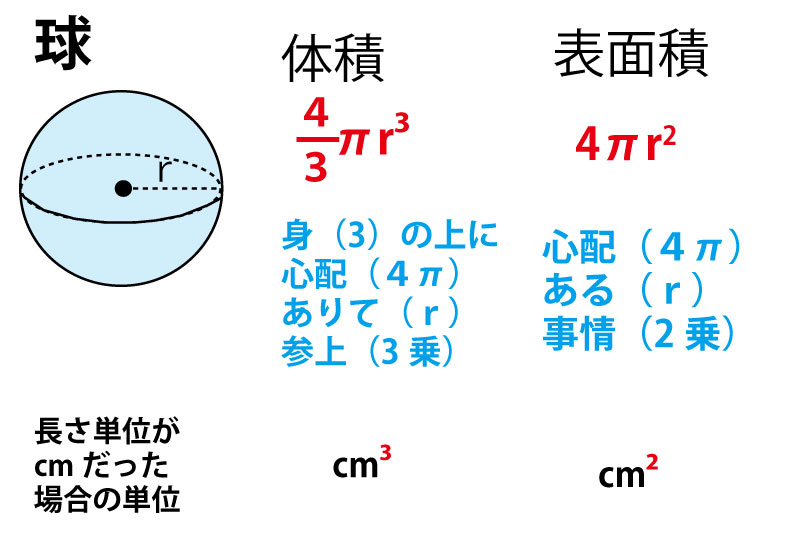
球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して愛されし者 側 面積 求め 方 壁紙 配布 球体 表面積 求め 方 球体 表面積 求め 方球の表面積比と体積比 ここでは球の表面積比と体積比について説明します。 ちなみに、基本的に球はすべて相似な図形です。 半径がrの球と、半径がkrの2つの球があったとし球体 の 体積 の 求め 方球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせ
半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め 底面の半径が r 1 r_1 r 1 ,天面の半径が r 2 r_2 r 2 ,高さが h h h である球台の体積は, V = 1 6 π h ( 3 r 1 2 3 r 2 2 h 2 ) V=\dfrac{1}{6}\pi h(3r_1^23r_2^2h^2) V = 6 1 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売
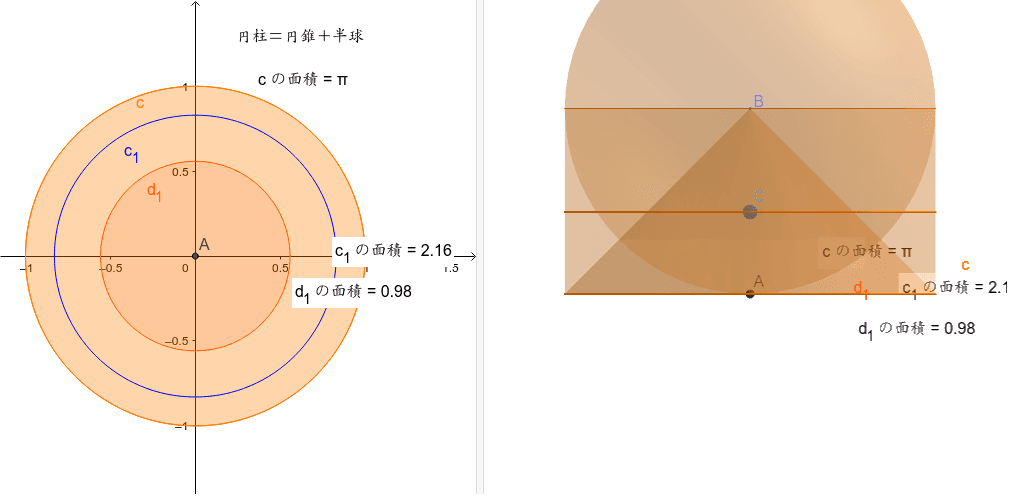



球の体積の求め方 Geogebra
解答 1 基本計算モードを選択。 2 球の体積の式4π× () 3 /3を入力。 3 答えを求める。 これより地球の体積は約x10 12 立方kmであることがわかる ひどい 球体 体積 求め 方 角錐 円錐の体積と表面積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを 球体の表面積S = 4πr 2




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



ユニーク球 表面積 求め 方 最高のぬりえ
球の体積V = 4 3πr 3球体の体積積分で求める方法 うちーノート 中学数学球の体積の求め方の公式を1発で覚 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式がある球の体積の求め方でなぜ3分の4が出てくるのかわかりません。 中1でもわかるように説明お願いします(>人<;) 縮め る球の表面積と体積 解く前に確認しよう ④ 球の表面積 半径が7の球の表面積をねと




球冠 Wikipedia




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
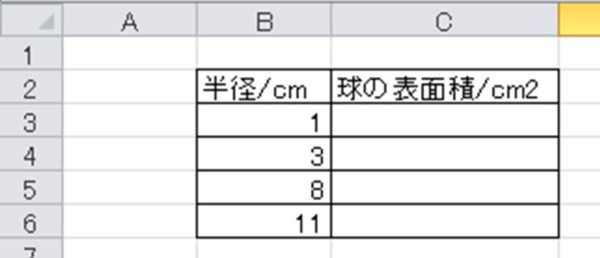
同様に球の体積をエクセルで求めていく方法を以下で確認していきます。 なお、上の例では円周率を有効数字3桁までとした314を用いましたが、厳密な計算が必要な場合はエクセル関数である PI関数(パイ関数) を使用するといいです。 1:球の体積の求め方(公式) まずは球の体積の求め方(公式)を紹介します。 下の図のように、 半径rの球があるとき、球の体積は4πr 3 / 3 となります。体積 = 一辺 × 一辺 × 一辺
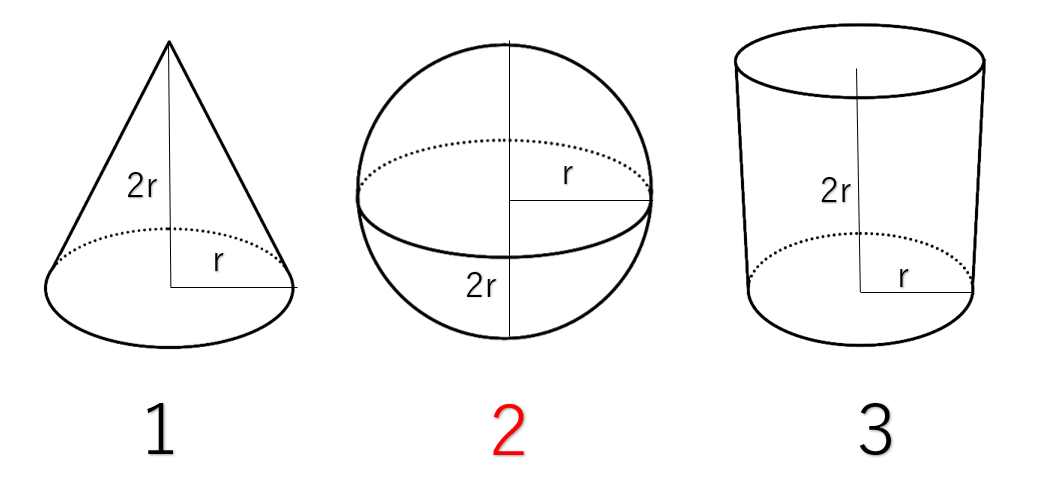



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




球の体積の求め方 感じる科学 味わう数学
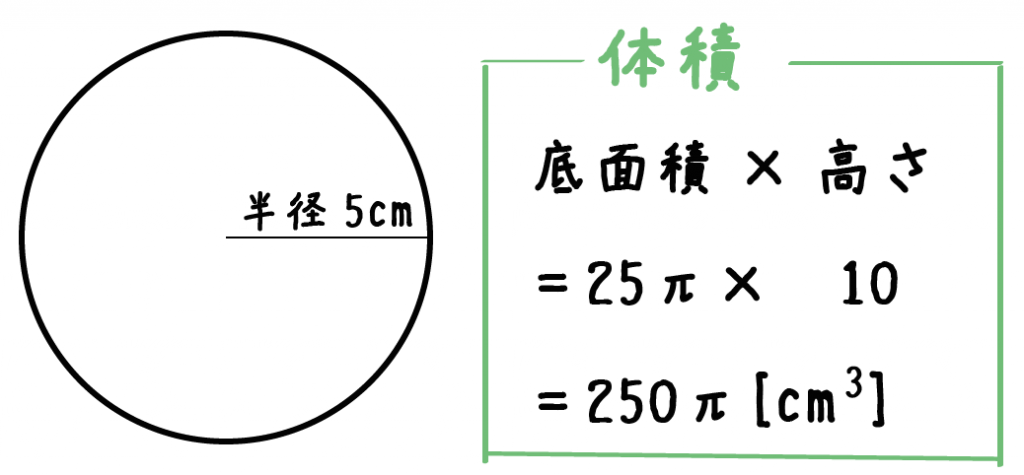
上で復習した面積の求め方と同様にして3乗の値を求めたら、それを球の体積を求める公式すなわちV=⁴⁄₃πr³に当てはめます。 式は V=⁴⁄₃πx1 となります。 たとえば半径が2cmの場合、半径を3乗すると、2 3 すなわち2x2x2となり、求める値は8になります体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の体積の公式 求め方や覚え方のコツを紹介するよ 中学や高校の数学の計算問題
①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r 新しい 球体 体積 求め 方 計算しない方が賢い時がある 苦手な数学を簡単に 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを体積を数値積分で求めることを考えてみましょう。ここでは球の体積を求めること を考えます。 まず、 高校の数学3の復習です。平面に半径1の円を描き、 それをx軸もしくはy 軸について回転させれば、半径1の球が出来上がります。したがって、この性質を




球の体積と表面積 Youtube




球の体積 表面積 中1数学 空間図形9 Youtube
楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。Dxdydz = abcdudvdw ⋅⋅⋅ (34) d x d y d z = a b c d u d v d w ⋅ ⋅ ⋅ ( 34) だから求めたい体積は、 V = ∫ ∫ ∫ dxdydz = abc∫ ∫ ∫ dudvdw V = ∫ ∫ ∫ d x d y d z = a b c ∫ ∫ ∫ d u d v d w もうここまで来たら、 dudvdw d u d v d w を積分した値は「半径1の球の体積と同じ ( 4 3π13 4 3 π 1 3 )」だから、 V = 4 3πabc ⋅⋅ ⋅(35) V = 4 3 π a b c ⋅ ⋅ ⋅ ( 35) と、公式通りになりました。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体



1




モヤモヤからワクワクへ 乱数 モンテカルロ法 を使って球の体積を求めてみよう Pythonを使う
最初の小節を2番目の小節に貸します。結果は、球体の体積です。 たとえば、球体が水没すると、水位が100 mlから625 mlに上昇するとします。したがって、球体の体積は525 mlです。 1 ml = 1 cmであることに注意してください。 パート2体積から質量を計算する球体 の 表面積 の 求め 方 暗号 アルファベット 数字 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすくの共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 平成21年12月2日




球の表面積と体積の公式 数学fun



Yogb6 Tjpto Wm
球の体積の求め方を忘れていたので活用させていただきました。 1149 女/歳代/会社員・公務員/非常に役に立った/ 使用目的 球体の24金の体積を求めるのに使用しました。 1034 女/歳代/主婦/役に立った/ 使用目的




Mathematics 球の体積と表面積を求める公式 働きアリ
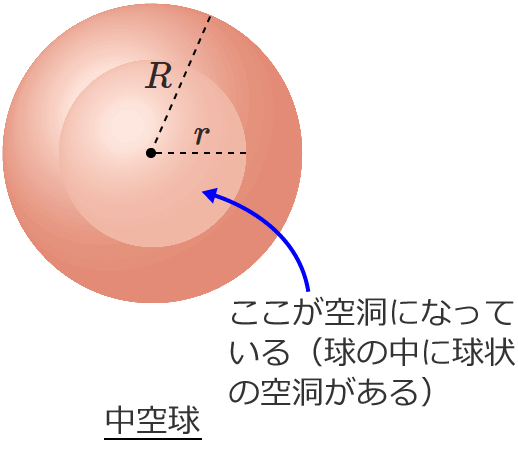



立体の体積を求める公式



1




球の体積と表面積 数学i フリー教材開発コミュニティ Ftext



球の体積を重積分で求めたいのですが 上手くいきません は球の上半分 半球 Yahoo 知恵袋



球の体積と表面積を積分で証明 高校数学の美しい物語




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




中1数学 球 例題編 映像授業のtry It トライイット




球の表面積の求め方 公式と計算例




球の体積と表面積 公式と計算問題と証明 Irohabook



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




中1 数学 中1 84 球について Youtube




球の体積公式の微分が表面積になっている理由 Youtube




球の表面積と体積の公式 数学fun



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球の体積と表面積を積分で証明 高校数学の美しい物語



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



数学 球の表面積を積分で計算してもうまくいかない人へ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の表面積 なぜ




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




球の表面積 体積 身勝手な主張




中1 数学 6 5 球の体積 表面積 Youtube




半球の体積と表面積を計算する 具体例で学ぶ数学



Excel エクセルで球の体積と表面積を計算する方法 モッカイ




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




2 を教えてください Clear



球の体積 簡単に計算できる電卓サイト




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



球の表面積の公式の求め方




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



2




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ



球の体積の積分 Geogebra



球の問題 苦手な数学を簡単に




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




球の表面積と体積の公式 数学fun



研究




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



大学入試問題




球の表面積の公式について みたにっき はてな




中1数学 球 練習編 映像授業のtry It トライイット




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積 Jsciencer




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




角錐 円錐の体積と表面積の公式 数学fun




球の体積 表面積の求め方 公式 小学生 中学生の勉強



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear
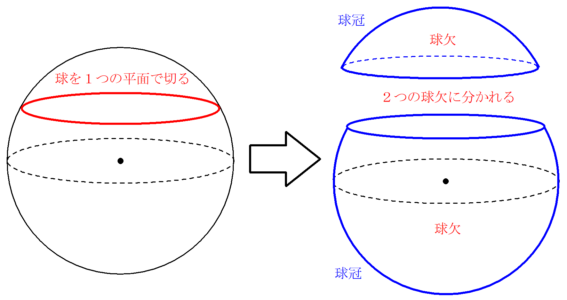



球欠と球冠 Fukusukeの数学めも




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




球の表面積と体積の公式 数学fun




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




これまでで最高の面積 球 の 体積 の 求め 方 最高のぬりえ



立体 の 表面積 求め 方




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



中1数学 球の表面積と体積の求め方と練習問題 Atstudier




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




初等幾何 球の表面積を求める 大人が学び直す数学




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要




球に関する公式 理数系無料オンライン学習 Kori



球の体積 高精度計算サイト




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト



1
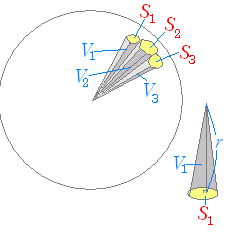



例題対比 球の体積と表面積




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積 球の表面積の公式の導出 積分 優技録




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clear




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ
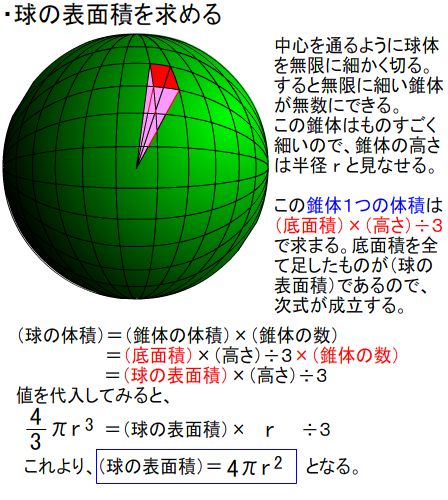



用語与太話 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ




球の体積 表面積 無料で使える中学学習プリント




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
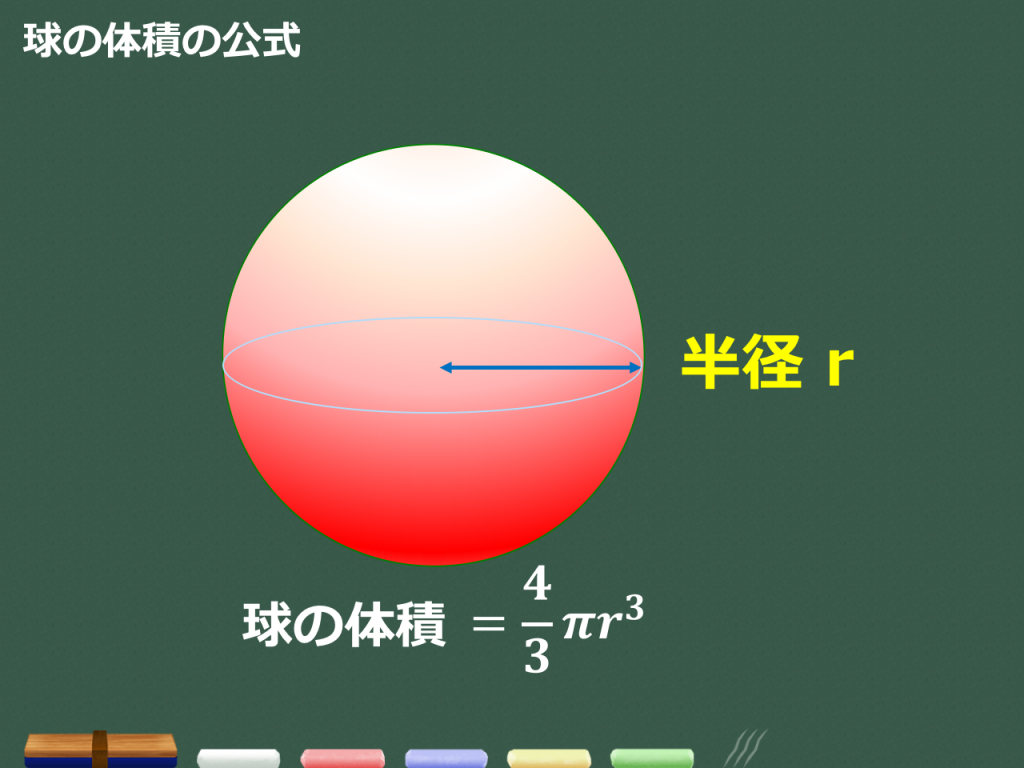



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun


