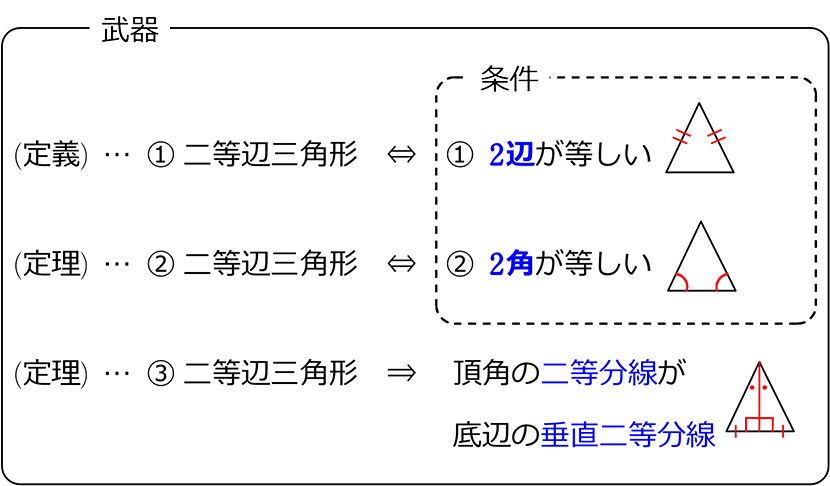
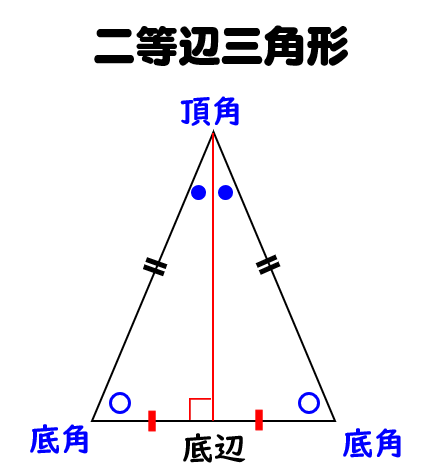
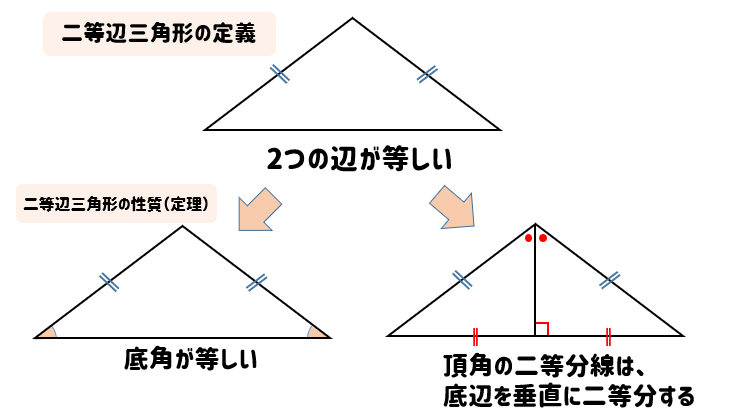
動画で学習 2 二等辺三角形になるための条件 数学 もう一度見る Play Video Play Mute Current Time 000 / Duration Time 000 Loaded 0%二等辺三角形になる条件 を考え、性質を逆に見た ものであることを理解す る。 二角が等しい三角形が二等辺 三角形であることを見いだし 証明する。 定理の逆について理解し、 その真偽を判断できる。 命題の逆について考え、逆が②二等辺三角形の性質 ⑴二等辺三角形の2つの底角は等しい。 ⑵二等辺三角形の頂角の二等分線は、底辺を垂直 に二等分する。 ③二等辺三角形になるための条件 2つの角が等しい三角形は、二等辺三角形である。 $ % 底辺 頂角 底角 3 特別な二等辺三角形
教科書に 二等辺三角形になるための条件 として 定理 三角形の Yahoo 知恵袋
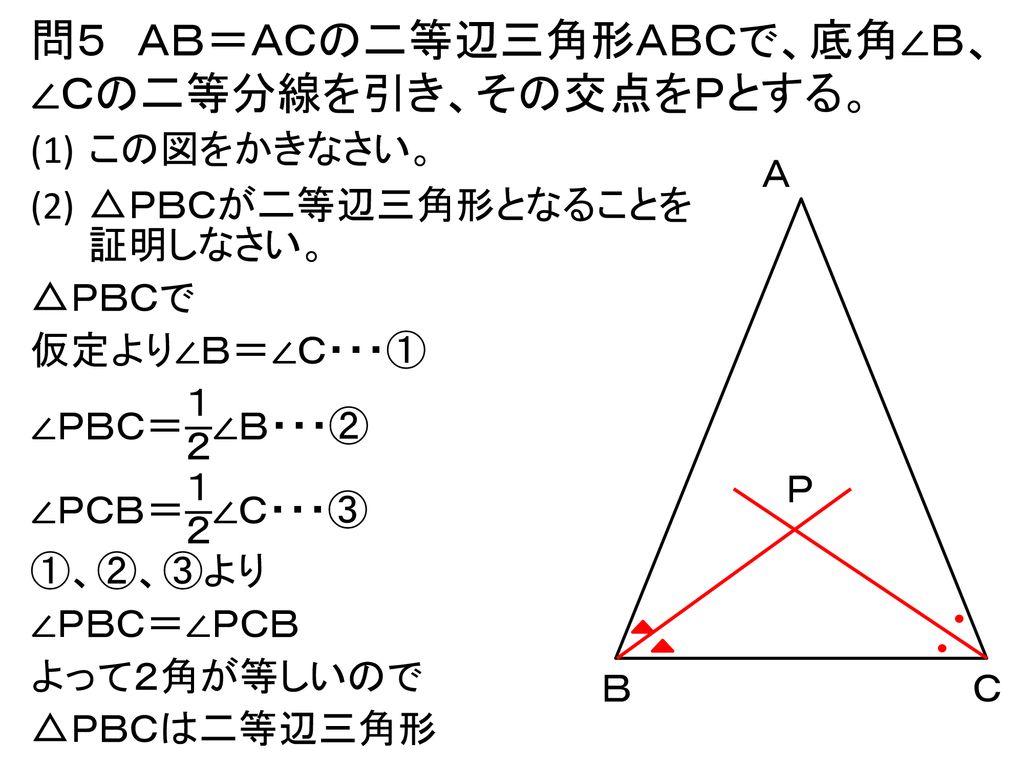
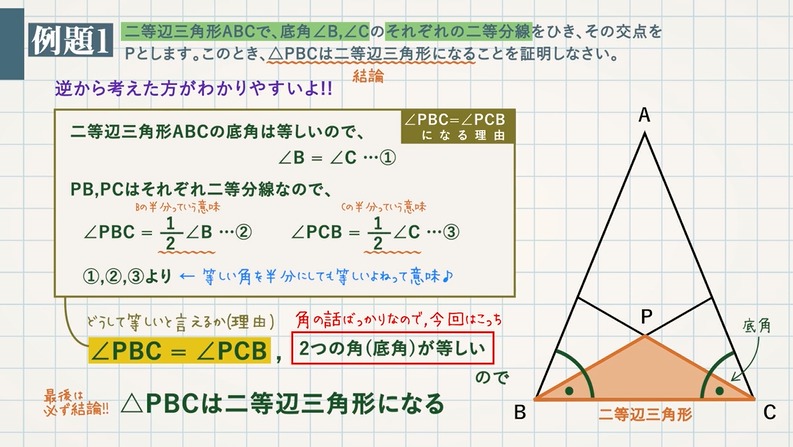
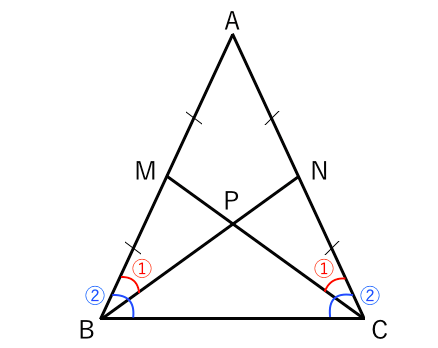
二等辺三角形になる条件
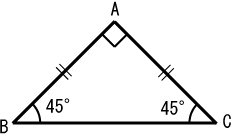
二等辺三角形になる条件-二等辺三角形のうち、頂角が直角に等しいものを直角二等辺三角形という。 直角二等辺三角形の場合、直角をはさむ 2 辺が等辺にあたり、斜辺が底辺にあたる。 底角の大きさはそれぞれ 45 度となる 三角形が二等辺三角形であることを証明するためには、次のどちらかを示せばよいことを覚えておきましょう。 二等辺三角形の成立条件 \(2\) つの辺の長さが等しい




二等辺三角形の性質と証明 無料で使える中学学習プリント
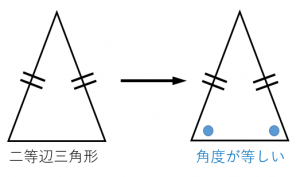
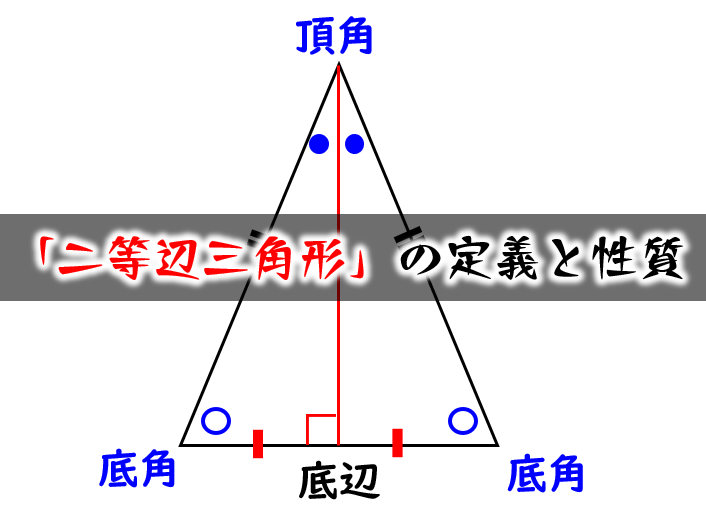
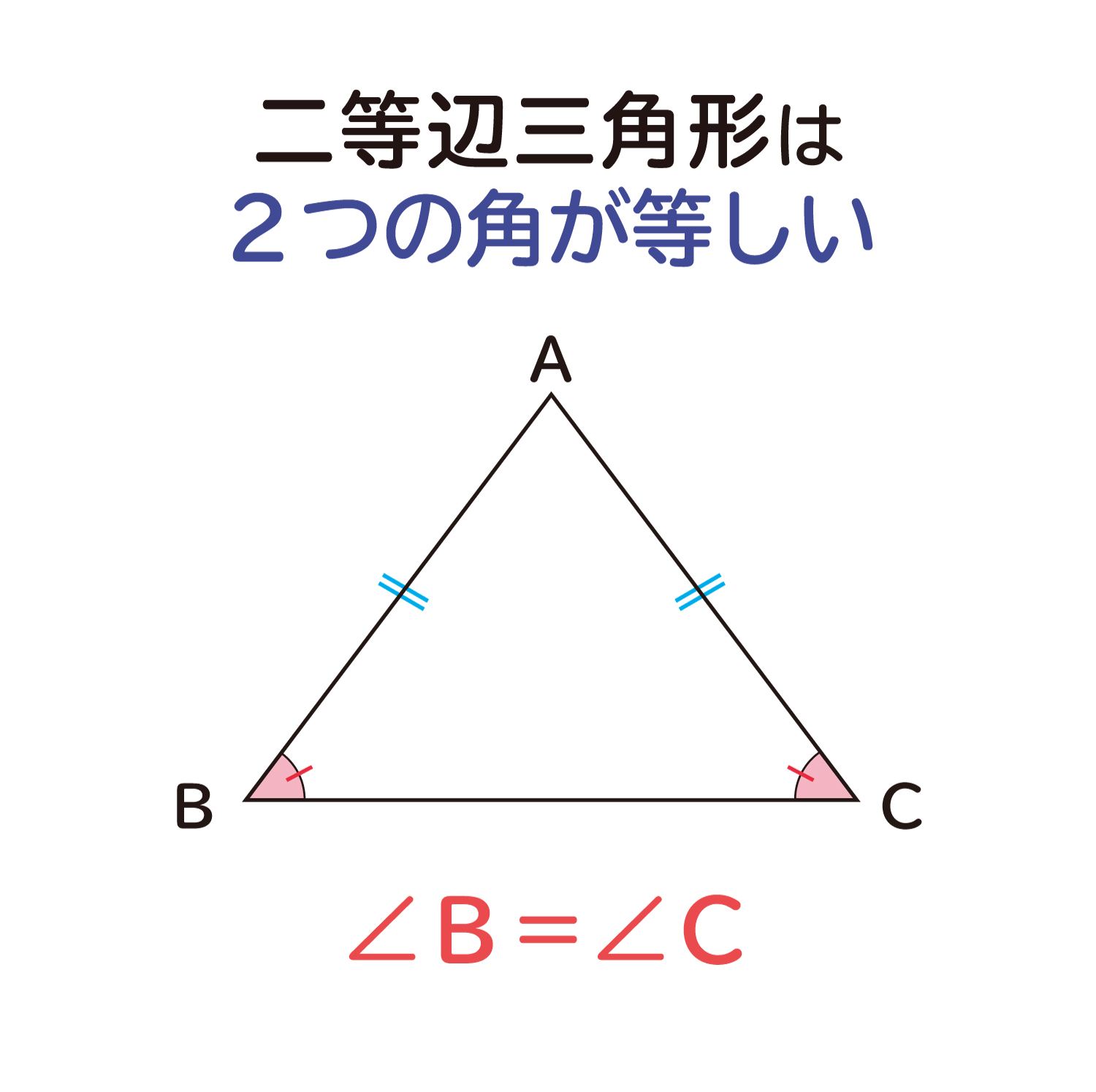
二等辺三角形の定義、定理、基本的な証明問題の練習プリントです。定期テストにもよく出題されますので、確実に出来るようにしましょう。 二等辺三角形の定義「二つの辺の長さが等しい三角形」 等しい二辺の間の角を頂角という。 頂角に向い合う辺を底辺という。二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。② 逆は「 ABC で,∠B=∠C ならば,AB=AC である。」である。2 つの角が等しい三角 形は二等辺三角形になるので,正しい。 ③ 逆は「2 つの直線 l, m に別の1 つの直線が交わるとき,同位角が等しいならば, l と m は 平行になる。」である。これは正しい。
中津市立東中津中学校2年数学「三角形」二等辺三角形になる条件 河野秀男教諭 Tweet 印刷用ページを表示する 掲載日:18年7月19日更新 学力向上支援教員・指導教諭らによる優れた授業をお届けする「シリーズ授業まるごと! 赤い部分が二等辺直角三角形になるのはなぜ? 教員採用試験の問題集にあり、恥ずかしながら自分にはわからなかったので質問です。 正方形の中に、正三角形が図のように内接しているとします。 そのとき、赤い三C において,a が最大のとき (i) a;
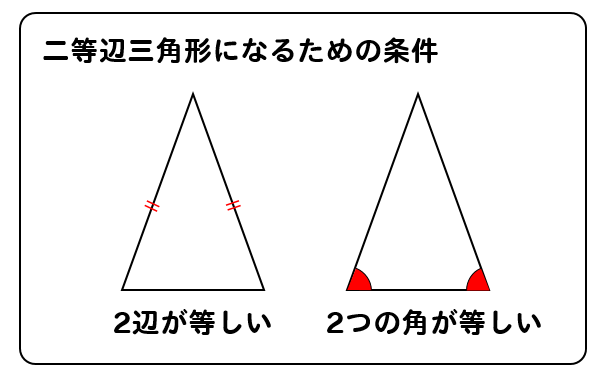
二等辺三角形 二等辺三角形の定義 二辺の長さが等しい三角形を二等辺三角形という。 二等辺三角形の性質 ① 二等辺三角形の2つの底角は等しい。 ② 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 ③ 二辺の長さが等しい三角形は二等辺三角形である。 1つの辺の長さとその両端の角の大きさが決まると、三角形は1通りに決まるので、この条件を満たせば、2つの三角形は合同です。 3つの合同条件に共通することは、 辺と角を合わせて3か所が等しい ということです。三角形の成立条件を前提としなければならないのか? 実は,直角三角形,鋭角三角形については,この前提は不要である.a2 ≦ b2 c2 からa < bc を導くことができるからである. 定理 正の数a;




どうやって証明すればいいですか 教えてください お願いします 人 Clear



本時のねらい 二等辺三角形の作図から証明を使って性質を導くことができる 定義や定理の用語の意味を理解する Ppt Download
・二等辺三角形になるための条件に関心を持ち,それを考えようとしている。関心・意欲・態度 ・二等辺三角形になるための条件について考察し,証明することができる。 見方・考え方 準備物 (教師)付箋紙,のり,テレビ,sd カード 二等辺三角形の条件はもう一つあります。 二つの辺の長さが等しい ← 二等辺三角形ですから当然ですね。 平行四辺形の条件では ・2組の対辺がそれぞれ等しい ですが、二等辺三角形の角の条件から類推して考えると二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ




二等辺三角形になるための条件 まなびの学園




この問題を解いてください Clear
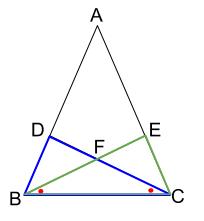
ABC が b = c の二等辺三角形であれば、底角 ∠B = ∠C であり(二等辺三角形の底角の性質)、逆に、 ABC の 2 角が ∠B = ∠C であれば、b = c の二等辺三角形となる(二等辺三角形の成立条件)。二等辺三角形2 2 2 右の図で abcはab=acの二等辺三角形で、bd=ceである。また、cdとbeの交点をfとするとき fbcは二等辺三角形になることを証明しなさい。直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




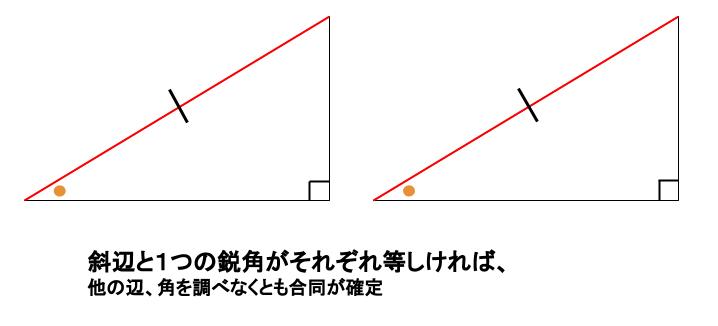
直角三角形の合同条件とその証明 数学fun
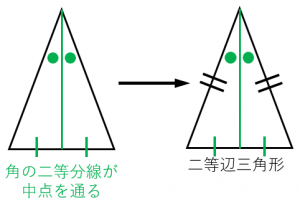
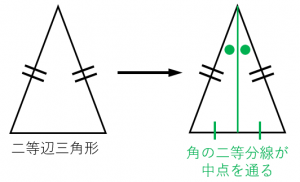
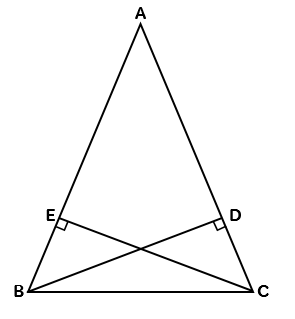
1 : 2 つの底角は愛しい 2 :頂角の二等分線は、底辺を垂直に二等分する 二等辺三角形になるための条件 (定義と定理を使う) ・ 2 辺が等しい ・ 2 つの角 (底角)が等しい このどちらかを証明できれば、二等辺三角形だと言えます。 1:23 例題 1 二次に, 三角形の合同条件(3 辺相等) が成り 立てば,2 つの三角形は合同であることの証明 について述べる。この証明は, 二等辺三角形 の底角定理を使って以下のように証明するこ とができる。 (証明) abc と dce において,ab=de, bc=ef, ca=fd ならば abc ≡ def・二等辺三角形になるための 条件,性質の逆と見ること ができる。数・考 視点1 指導計画の工夫 付せん紙を図のように折り 曲げ,重なったときにできる ief が二等辺三角形にな る。 をうめて証明を完成さ せなさい。 証明



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



二等辺三角形
有料講座 応用問題 二等辺三角形になるための条件について学習します。 無料講座基本の解説約4分08秒 有料講座基本の解説・基本問題の解説・応用問題まで約9分58秒 応用問題応用問題の解説約8分40秒 ※無料講座の続きは、有料講座二等辺三角形は2つの辺の長さが等しいことで、上のような性質が出てきます。これらの性質がそれぞれ正しいことを確認してみましょう。今回はその2つ目の性質の 頂角の二等分線は、底辺を垂直に二等分する こと確認していきたいと思います。 参考:二等辺三角形の1つ目の性質「2つの角は間 ・ 二等辺三角形の2つの底角が等しいことを証明することができる。 ・ 定義、頂角、底辺、底角の意味を理解する。 教科書108、109ページの「とびらの問題」の名札立てをつくり、様々な三角形を見付け、それがどのような三角形であるかを示させる




二等辺三角形の性質と証明 無料で使える中学学習プリント



31investment Com Wp Content Uploads 16 10 8ce
二等辺三角形 になるための 条件 二等辺三角形に なるための条件 を考察し,証明す ることができる。 ある定理の逆を いうことができ, それが成り立つ かどうかを調べ ることができる。 定理の逆の意味を 理解している。 二等辺三角形にな るための条件を理 解している。 3T:「『 二等辺三角形になるための条件』といいます. 三角形が二等辺三角形とまだわかっていない ときに使うので『2つの角』と表現します.」三角形の成立条件とその証明 レベル ★ 基礎 平面図形 更新日時 三角形の成立条件(存在条件):三辺の長さが a, b, c a,\b,\c a, b, c である三角形が存在する必要十分条件は, a b > c ab > c a b > c かつ




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su
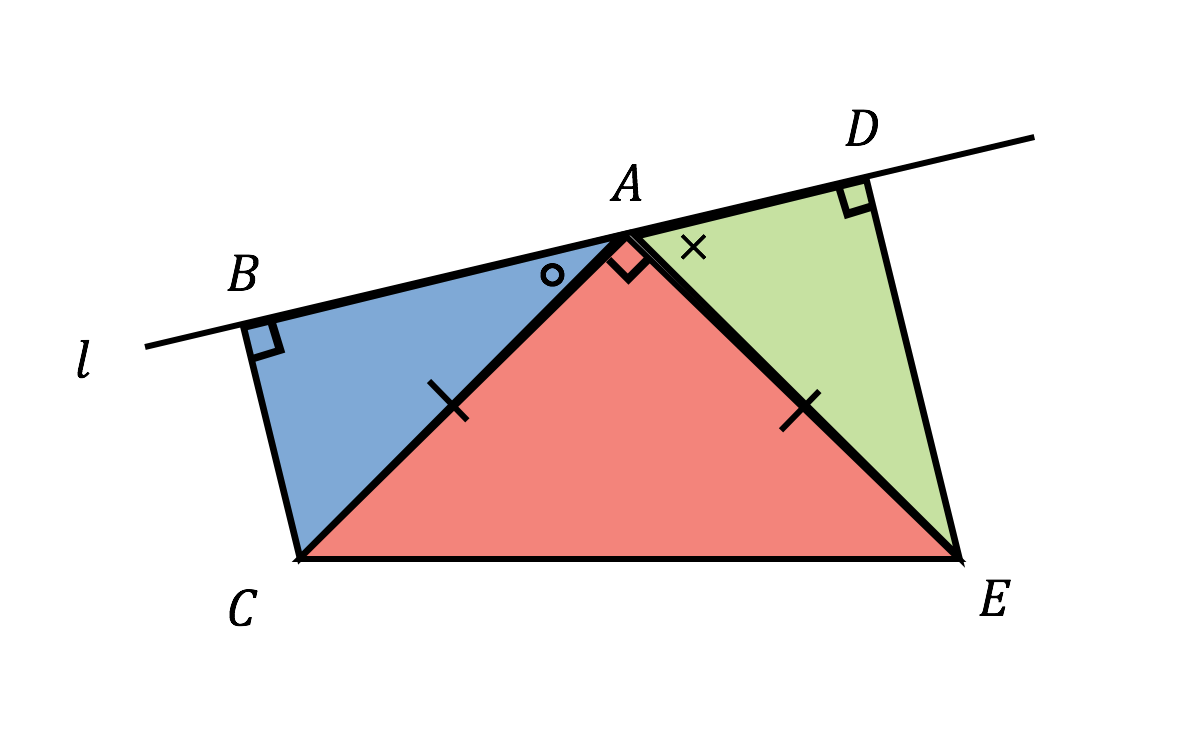
\(\triangle BEF\) は \(2\) つの角が等しいので、二等辺三角形であることがいえます。 これを解答にします。 角度が等しいことをていねいに順序立てて説明します。 解答 仮定 \(AD=AE\) より、\(\triangle AED\) は二等辺三角形である。 二等辺三角形になるための条件で、 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角とする二等辺三角形である。 と、 2つの角が等しい三角形は二等辺三角形である。 この二つは同じ意味・根拠ですか?こんにちは、ウチダショウマです。




โน ตของ 二等辺三角形になるための条件 ช น Junior High数学 Clear




二等辺三角形になることの証明 Youtube




直角三角形の合同条件とその証明 数学fun



Http Www Fdtext Com Dat Suub2 4zukei 2goudou Pdf



中学数学 図形の合同 図形の性質



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



1




三角形の成立条件を理解するたった1つのポイント わかりやすく解説 遊ぶ数学



この三角形が二等辺三角形になるとこを簡単に説明してください Yahoo 知恵袋




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形と証明 Youtube



二等辺三角形の定義と性質 問題の解き方 数学fun



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



教科書に 二等辺三角形になるための条件 として 定理 三角形の Yahoo 知恵袋



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
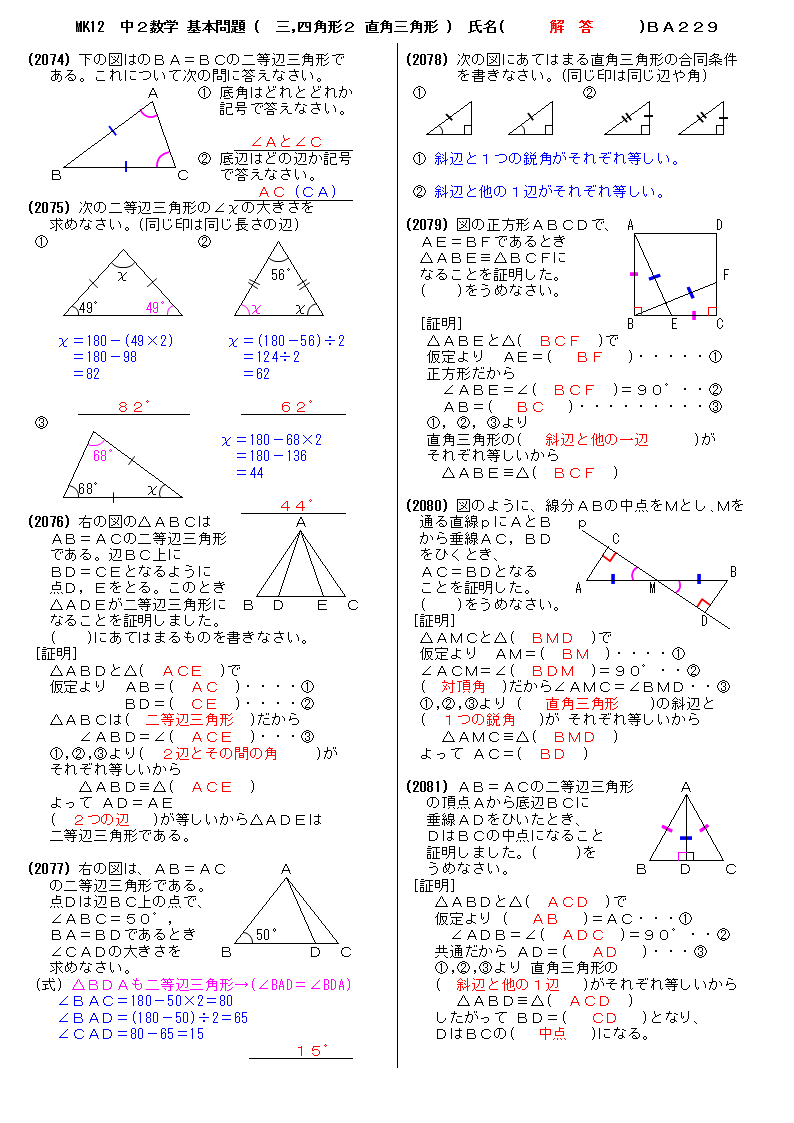



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
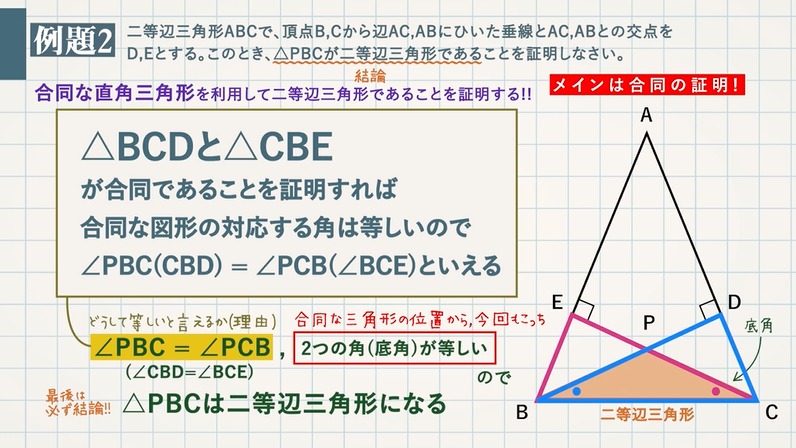



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



1



2 57第4章 二等辺三角形 二等辺三角形になるための条件 フロントエンドなブログ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



中学2年数学練習問題 二等辺三角形になる条件 証明 角度を求める



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題
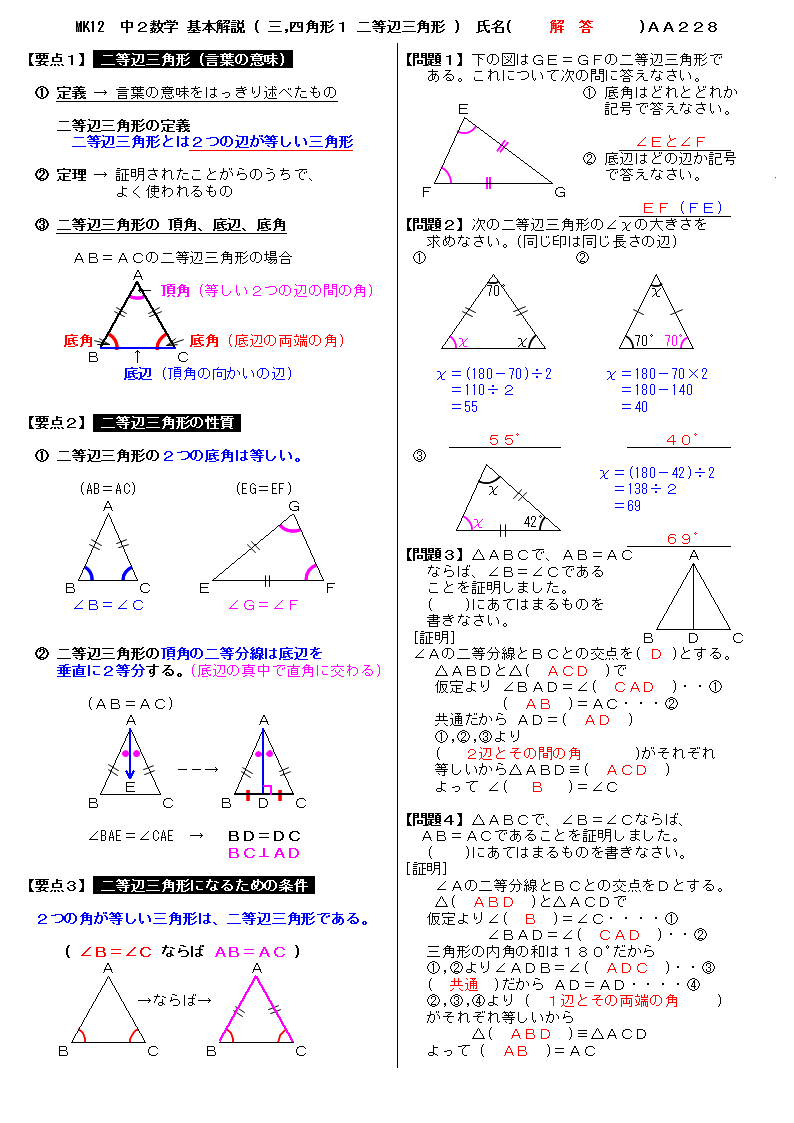



無料 中2数学 基本解説 解答プリント 228 三角形 四角形1 二等辺三角形



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




中二数学5章1節2の2二等辺三角形になるための条件2二周目 Youtube




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形の証明の答えと解説お願いします Clear



中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su




二等辺三角形になるための条件 中2数学 三角形と四角形2 Youtube



1




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




中2の証明問題を解く上で 必要な知識をまとめました プリントダウンロードできます 東大に文理両方で合格した男が綴る 受験の戦略



二等辺三角形と正三角形 算数用語集




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath




二等辺三角形になるための条件 Youtube




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
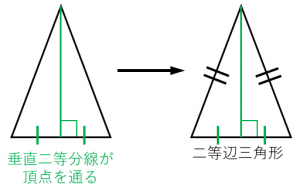



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




二等辺三角形 2つの角が等しくなることの証明 Youtube
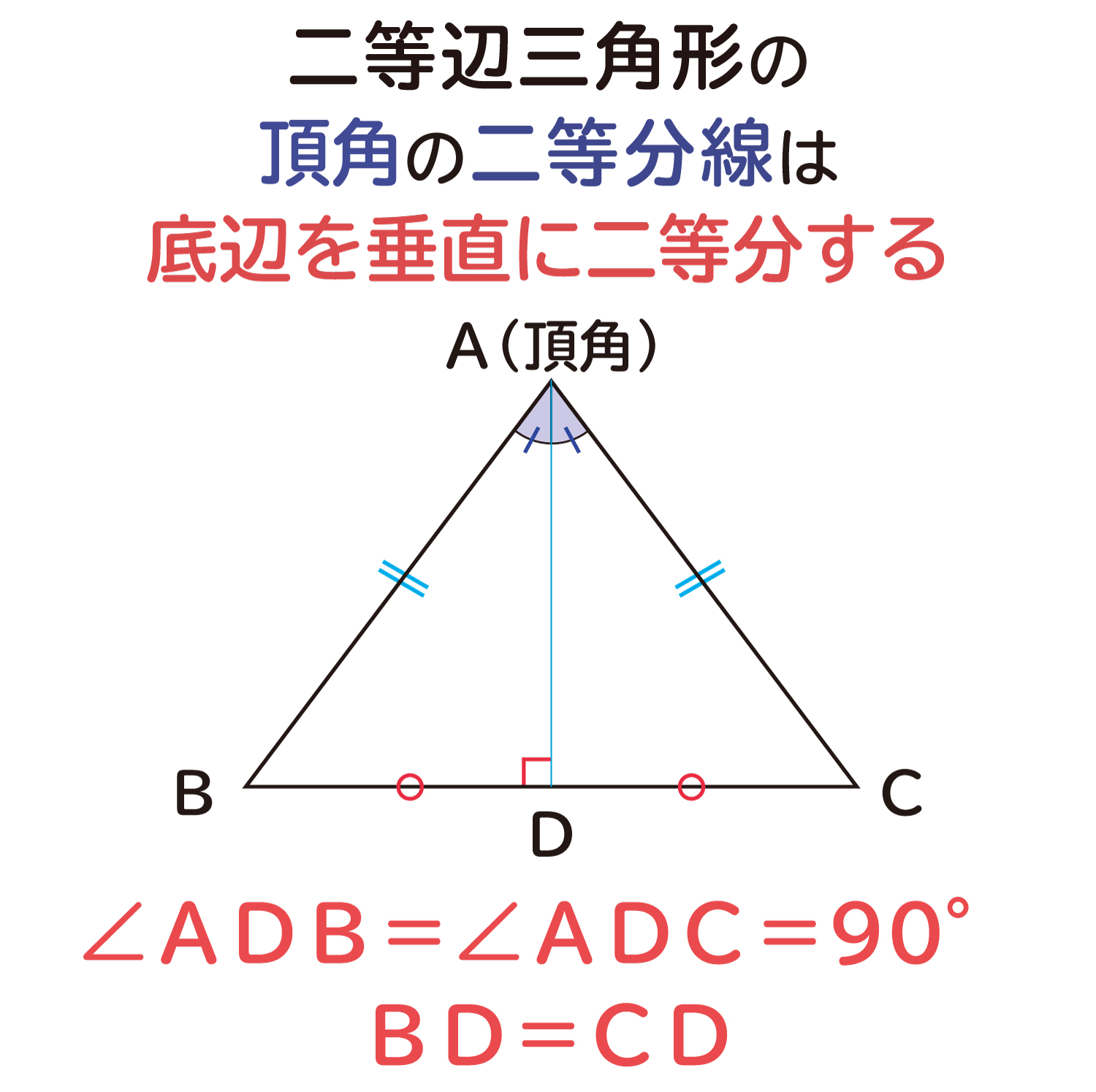



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル
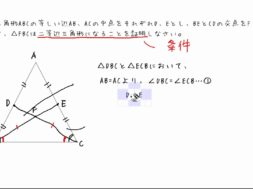



中2数学 08 7 二等辺三角形になることの証明 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



正三角形は二等辺三角形に入るんですか 問題について 宿題の認知科学 広瀬 友紀 Webちくま



数学 二等辺三角形になるための条件 タイトル この問題 Yahoo 知恵袋



二等辺三角形の定義と性質 問題の解き方 数学fun



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




二等辺三角形 Wikipedia




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




中2 二等辺三角形の性質 中学生 数学のノート Clear



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




二等辺三角形と証明 Youtube




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題



二等辺三角形の2つの角は等しくなる ことの説明 おかわりドリル



2つの相似な二等辺三角形が図のように1辺を共有しています Aとdはそれぞれ着色された領域です A D 9 が成立するときの Cos A の値は Quora



3年算数三角形教え方のポイント



直角二等辺三角形 Wikipedia




無料 中2数学 発展問題 解答プリント 228 三角形 四角形1 二等辺三角形



1




三角形の成立条件を理解するたった1つのポイント わかりやすく解説 遊ぶ数学




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月




定理 二等辺三角形の両底角は等しい を使って 身勝手な主張



二等辺三角形の性質を利用した合同の証明 チーム エン



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




中2数学 二等辺三角形の証明 練習編 映像授業のtry It トライイット




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形になるための条件 Youtube
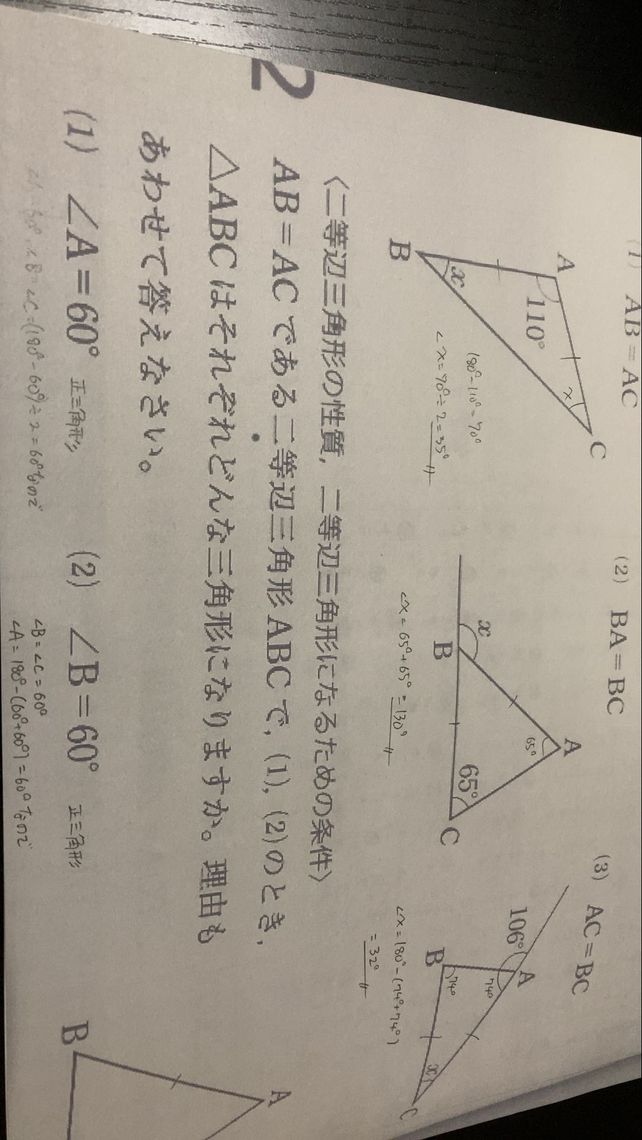



Abac 2 Babc 3 Acbc Lihat Cara Penyelesaian Di Qanda
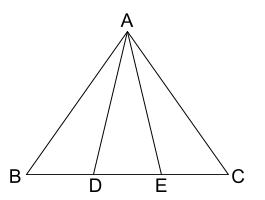



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su




二等辺三角形の性質 Youtube




ae Descubre Como Resolverlo En Qanda



三角形の証明二等辺三角形や正三角形の証明の問題を解いてください Yahoo 知恵袋




中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット



Http Cms Oklab Ed Jp Jh Rokuhoku Index Cfm 1 1423 C Html 1423 1217 Pdf




二等辺三角形の性質と証明 無料で使える中学学習プリント
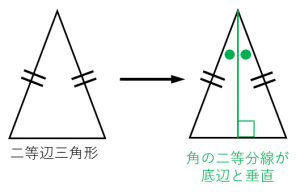



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




Tossランド 二等辺三角形になるための条件
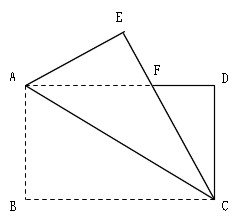



Mathematics 二等辺三角形 二等辺三角形になることの証明 働きアリ




三角形の成立条件を理解するたった1つのポイント わかりやすく解説 遊ぶ数学




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




中2 二等辺三角形の性質 中学生 数学のノート Clear


